Interpretable-Machine-Learning

5.8.1整体思路

假设以下场景：

您已经训练了机器学习模型来预测公寓价格。对于特定公寓，它预测为300,000欧元，现在你需要解释这个预测结果。公寓面积为50平方米，位于二楼，附近有一个公园，公寓里不准养猫：

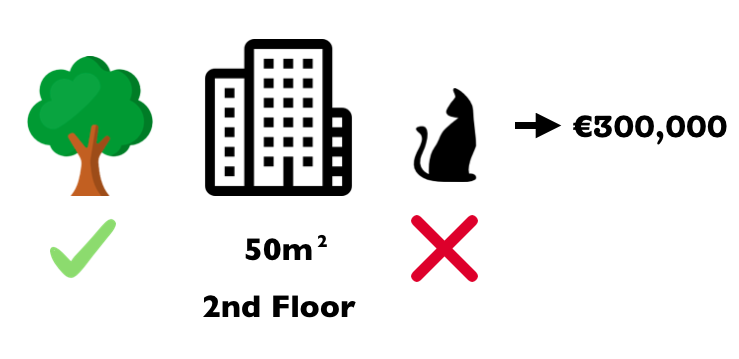
所有公寓的平均预测为310,000欧元。与平均预测结果相比较，每个特征值对该预测结果的贡献是多少？

线性回归模型的答案很简单。每个特征的效果是特征的权重乘以特征的取值。这仅适用于线性模型。对于更复杂的模型，我们需要不同的解决方案。例如，LIME 使用局部模型来估计影响。另一种解决方案来自合作博弈理论：由Shapley（1953）>39 创造的Shapley值是一种根据球员对比赛结果的贡献来为球员分配收入的方法（球员通过在联盟中合作并从这种合作中获得一定的收入）

在这个问题里，球员、比赛、收入分别是什么？这与机器学习预测和可解释性有什么联系呢？ “比赛”是数据集的单个实例的预测任务。 “增益”是该实例的实际预测减去所有实例的平均预测。 “球员”是协作接收增益的实例的特征值（=预测某个值）。在我们的公寓示例中，附近的公园，猫禁令，50平米和2楼的特征值共同实现了预测结果300,000欧元。我们的目标是解释实际预测（300,000欧元）和平均预测（310,000欧元）之间的差异：相差10,000欧元。

答案可能是：附近的公园贡献了30,000欧元; 50码贡献了10,000欧元;2楼贡献了0欧元;猫禁令贡献 - 50,000欧元。总共加起来 - €10,000，即最终预测结果减去平均预测的公寓价格。

我们如何计算一个特征的Shapley值？

Shapley值是一个特征值在所有可能组合中的平均边际贡献。清楚了吗？

在下图中，我们解释如何评估<font color=gray size=72>猫禁令</font>这一特征值在添加到<font color=gray size=72>附近有公园</font>和<font color=gray size=72>50平米</font>的组合时的贡献。我们假设< font color=gray size=72> 附近有公园</font>,<font color=gray size=72>猫禁令</font>和<font color=gray size=72>50平米</font>构成了一个组合，通过从数据中随机抽取另一个公寓并使用其值来消除地板特征的影响。然后我们预测带这种组合的公寓价格（310,000欧元）。在第二步中，我们从组合中去掉<font color=gray size=72>不准养猫</font>的特征，并把它置换成一个随机值（禁猫／允许猫），来估计< font color=gray size=72> 附近有公园</font>和<font color=gray size=72>50平米</font>这一组合的价值（€320,000）。因此，< font color=gray size=72>猫禁令</font>的贡献是310,000欧元 - 320,000欧元= –10,000欧元。该估计值取决于随机抽取公寓的价值，该公寓充当猫和地板特征的贡献的“评估者”。如果我们重复这个采样步骤并平均贡献，我们将得到更好的估计。

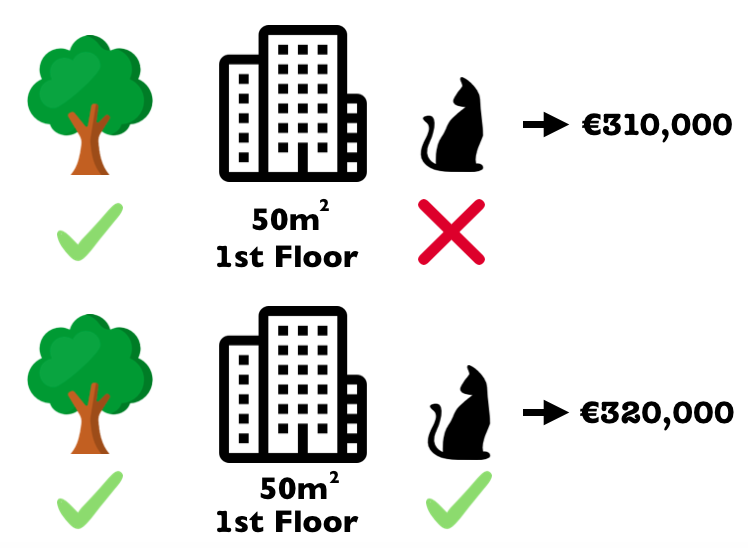
我们对所有可能的组合重复这个测算。 Shapley值是所有可能组合的所有边际贡献的平均值。计算时间随着特征的数量呈指数增长。保持计算时间可控的一种解决方案是仅对可能组合的少数样本计算贡献。

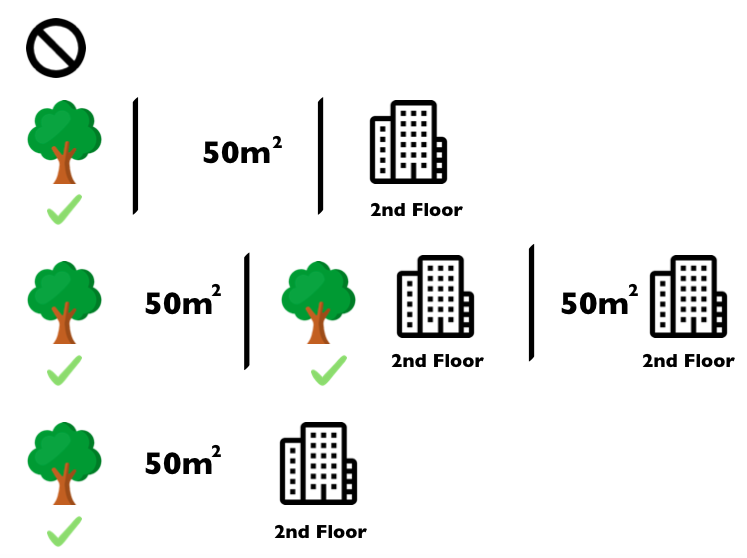
下图显示了确定<font color=gray size=72>猫禁令</font>的Shapley值所需的所有特征值的组合。第一行显示没有任何特征值的组合。第二，三和四行显示出不同的组合。随着组合内元素数目越来越大，以“

”分隔。总而言之，以下组合是可能的：

• 没有特征
• 附近有公园
• 50平米
• 第二层楼
• 附近有公园+50平米
• 附近有公园+第二层楼
• 50平米 + 第二层楼
• 附近有公园 + 50平米 + 第二层楼

对于每一种组合，我们分别计算包含和不包含特征<font color=gray size=72>不允许养猫</font>的预测公寓价格，并取其差值得到边际贡献。Shapley值是边际贡献的(加权)平均值。我们将不属于组合的特征值替换为来自公寓数据集的随机特征值，以获得来自机器学习模型的预测结果。

如果我们对所有特征值的Shapley值进行估计，我们就得到了预测值(减去平均值)在特征值之间的完整分布。